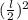Answer:
lw +
 × π ×
× π ×
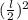 ⇒ Answer D is correct
⇒ Answer D is correct
Explanation:
First, let us find the area of the semi-circle.
Area =
 × π × r²
× π × r²
Given that,
diameter of the semi-circle is ⇒ l
∴ radius ⇒ l / 2
Let us find it now.
Area =
 × π × r²
× π × r²
Area =
 × π ×
× π ×
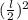
Secondly, let us find the area of the rectangle.
Area = length × width
Given that,
length ⇒ l
width ⇒ w
Let us find it now.
Area = length × width
Area = l ×w
Area = lw
And now let us find the total area.
Total area = Area of the rectangle + Area of the semi - circle
Tota area = lw +
 × π ×
× π ×