Answer:
D) 91
Explanation:
For the normal approximation, we need that:
np > 5 and np(1-p) > 5
In this question:
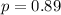
So
A) 10
n = 10, then
10*0.89 = 8.9 > 5
10*0.89*0.11 = 0.979 < 5
Does not satisfy.
B) 11
n = 11, then
11*0.89 = 9.79
11*0.89*0.11 = 1.0769 < 5
Does not satisfy
C) 30
n = 30
30*0.89 = 26.7
30*0.89*0.11 = 2.937 < 5
D) 91
n = 91
90*0.89 = 80.1
90*0.89*0.11 = 8.881 > 5
So this satisfies, and 91 is the answer