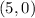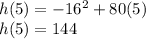Question

Which ordered pair cannot be a solution of h(t)=-16^2+80t If h is the height of a ball above ground after t seconds?

Answer 1

It seems that this question would make more sense if it were: Which ordered pair can be a solution of
`h(t)=-16^2+80t`

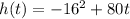
All alternatives but B) cannot be a solution for the function.

Explanation:

Here we have
`t=x`

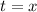
So, we may write the funtion as:
`h(x)=-16^2+80x`

`h(x)=y`

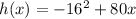
Let's test all the points:

A)
`(1, 64)`

`h(1)=-16^2+80(1)\\h(1)=-256+80\\h(1)=-176`

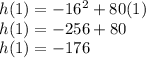
B)
`(2, 96)`

`h(2)=-16^2+80(2)\\h(2)=-256+160\\h(2)=96`

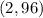
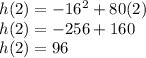
C)
`(-4, 256)`

`h(-4)=-16^2+80(-4)\\h(-4)=-256-320\\h(-4)=-576`

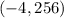
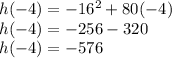
D)
`(5, 0)`

`h(5)=-16^2+80(5)\\h(5)=144`

Answer 2

NON of them can be a solution.

Explanation:

When I plugged them in to the equation they all came out false.