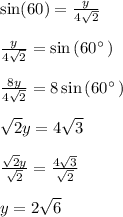Question

analyze the diagram below and complete instructions that follow find the value of x in the value of y ​

Answer 1

The values are
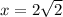`x=2√(2)` and
`y=2√(6)`.

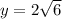Explanation:

A right triangle is a type of triangle that has one angle that measures 90°.

In a right triangle, the sine of an angle is the length of the opposite side divided by the length of the hypotenuse.

`\sin(\theta)=(opposite \:site)/(hypotenuse)`

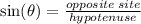
To find the value of x we use the above definition. From the diagram we can see that the angle is 30º and the hypotenuse is
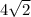`4√(2)`. Therefore,

`\sin(30)=(x)/(4√(2) )\\\\(x)/(4√(2))=\sin \left(30^(\circ \:)\right)\\\\(8x)/(4√(2))=8\sin \left(30^(\circ \:)\right)\\\\√(2)x=4\\\\(√(2)x)/(√(2))=(4)/(√(2))\\\\x=2√(2)`

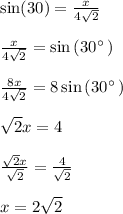
To find the value of y we use the above definition. From the diagram we can see that the angle is 60º and the hypotenuse is
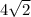`4√(2)`. Therefore,

`\sin(60)=(y)/(4√(2) )\\\\(y)/(4√(2))=\sin \left(60^(\circ \:)\right)\\\\(8y)/(4√(2))=8\sin \left(60^(\circ \:)\right)\\\\√(2)y=4√(3)\\\\(√(2)y)/(√(2))=(4√(3))/(√(2))\\\\y=2√(6)`