Question

The sum of the squares of two consecutive positive odd integers is 202. Find the numbers. Please use a let statement and algebraic solution. thanks! :)

Answer 1

9 and 11

Explanation:

The sum of the squares of two consecutive positive odd integers is 202.

Let first number be x and other number is (x+2).

According to question,

`x^2+(x+2)^2=202\\\\x^2+x^2+4+4x=202\\\\2x^2+4x+4=202\\\\2x^2+4x-198=0`

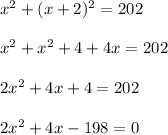
It is a quadratic equation. The solution of a quadratic equation is given by :

`x=(-b\pm √(b^2-4ac) )/(2a)`

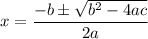
We have, a = 2, b = 4 and c = -198

So,

`x=(-b+ √(b^2-4ac) )/(2a), (-b- √(b^2-4ac) )/(2a)\\\\x=(-4+ √(4^2-4* 2* (-198)) )/(2(2)), (-b- √(b^2-4ac) )/(2a)\\\\x=9, -11`

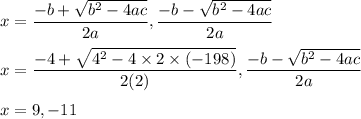
So, first positive odd integer is 9 and second one is (9+2)=11