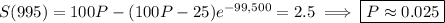Question

A 100 gallon tank initially contains 100 gallons of sugar water at a concentration of 0.25 pounds of sugar per gallon suppose that sugar is added to the tank at a rate of p pounds per minute that sugar water is removed at a rate of 1 gallon per minute and that water in the tank is kept well mixed. What value of P should we pick so that that when 5 gallons of sugar solution is left in the tank the concentration is .5lbs of sugar/gallon?

Answer 1

At the start, the tank contains

(0.25 lb/gal) * (100 gal) = 25 lb

of sugar. Let
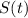`S(t)` be the amount of sugar in the tank at time
`t`. Then
`S(0)=25`.

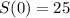Sugar is added to the tank at a rate of P lb/min, and removed at a rate of

`\left(1(\rm gal)/(\rm min)\right)\left((S(t))/(100)(\rm lb)/(\rm gal)\right)=(S(t))/(100)(\rm lb)/(\rm min)`

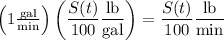
and so the amount of sugar in the tank changes at a net rate according to the separable differential equation,

`(\mathrm dS)/(\mathrm dt)=P-\frac S{100}`

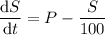
Separate variables, integrate, and solve for S.

`\frac{\mathrm dS}{P-\frac S{100}}=\mathrm dt`

`\displaystyle\int\frac{\mathrm dS}{P-\frac S{100}}=\int\mathrm dt`

`-100\ln\left|P-\frac S{100}\right|=t+C`

`\ln\left|P-\frac S{100}\right|=-100t-100C=C-100t`

`P-\frac S{100}=e^(C-100t)=e^Ce^(-100t)=Ce^(-100t)`

`\frac S{100}=P-Ce^(-100t)`

`S(t)=100P-100Ce^(-100t)=100P-Ce^(-100t)`

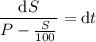
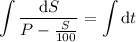
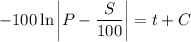
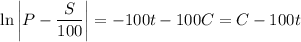
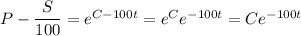
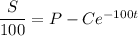
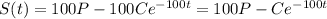
Use the initial value to solve for C :

`S(0)=25\implies 25=100P-C\implies C=100P-25`

`\implies S(t)=100P-(100P-25)e^(-100t)`

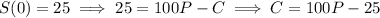
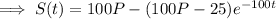
The solution is being drained at a constant rate of 1 gal/min; there will be 5 gal of solution remaining after time

`1000\,\mathrm{gal}+\left(-1(\rm gal)/(\rm min)\right)t=5\,\mathrm{gal}\implies t=995\,\mathrm{min}`

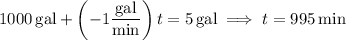
has passed. At this time, we want the tank to contain

(0.5 lb/gal) * (5 gal) = 2.5 lb

of sugar, so we pick P such that

`S(995)=100P-(100P-25)e^(-99,500)=2.5\implies\boxed{P\approx0.025}`