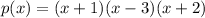Question

The polynomial p(x)=x^3-7x-6 has a non-factor of (x+1) rewrite p(x) as a product of linear factors.

Answer 1

Using synthetic division suffices to answer your question:

Explanation:

Synthetic division is the process by one reduces a large polynomial in your case
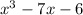`x^3-7x-6` by a binomial in your case
`(x+1)`.

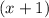To do so one does the following:

`\begin{array}{cccccc}-1|& 1&0&-7&-6\\ & &-1&1&6 \\& 1&-1&-6&0 \end{array}`

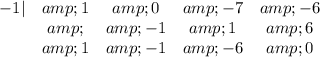
Since we divided by a linear binomial it reduces the power by one which produces the following quadratic:

`(x^2-x-6)`

Which can be factored in the following, and I will provide the complete factorization as well:

`p(x)=(x+1)(x-3)(x+2)`