Question

The accompanying Venn diagram illustrates a sample space containing six sample points and three events, A, B, and C. The probabilities of the sample points are P(1) = 0.3, P(2) = 0.2, P(3) = 0.1, P(4) = 0.1, P(5) = 0.1 and P(6) = 0.2.

Find:

Answer 1

Explanation:

To find the probability of a certain set, we must add the probability of the points that are contained in the specific set.

a) P(A): Add the probability of 1,3,5. That is P(1)+P(3)+P(5) = 0.5

b)
`P(A\cap B)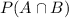`. This set has no points in it, so its probability is 0.

c) P(A\cup B \cup C): Add the probability of 1,2,3,4,5,6. So, it is 1.

d)
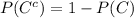`P(C^c) = 1- P(C)`. P(C) is the probability by summing 5,6,2 so P(C) = 0.5. So
`P(C^c)=0.5`

e)
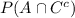`P(A\cap C^c)` That is, all the points that are in A but not in C. So add 1,3. Then the probability is 0.4

e')
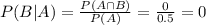`P(B|A) = (P(A\cap B ))/(P(A))=(0)/(0.5)=0`, using the definition of conditional probabily and results a,b.

f) Two events are mutually exlusive if the probability of their intersection is 0. In this case A and C are not mutually exclusive, since
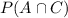`P(A\cap C)` is the probability of 5, that is 0.1. Since 0.1>0, they are not mutually exclusive.