Answer:
a) y = 0.459 m , b) t = 13 s
Step-by-step explanation:
a) For this exercise we use Newton's second law to find the acceleration of the block
we fix a reference system with the x axis parallel to the plane and the y axis perpendicular to it
X axis
-Wₓ - fr = m a (1)
Axis y
N -
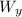 = 0
= 0
N = W_{y}
the friction force has the formula
fr = μ N
let's use trigonometry to find the components of the weight
sin 25 = Wₓ / W
Wₓ = W sin 25
cos 25 = W_{y} / W
W_{y} = W cos 25
we substitute in 1
- W sin 25 - μ W cos 25 = m a
- g (sin 25 - μ cos 25) = a
let's calculate
a = - 9.8 (sin 25 - 0.12 cos 25)
a - 0.25 m / s
this is the acceleration on the plane, so we can use the kinematic relations in one dimension
the highest point where the block rises the speed is zero (va = 0)
v² = v₀² - 2 a y
y = v₀² / 2g
y = 3 2 / (2 9.8)
y = 0.459 m
this is the distance the cantes block travels to stop
b) the time of the entire journey is
y = v₀ t - ½ a t²
the point where the body recesses is y = 0
0 = (vo - ½ a t) t
whose solutions are
t = 0
0 = vo - ½ a t
t = 2vo / a
t = 2 3 / 0.459
t = 13 s