Question

3) Smurfette is glad you're getting on with your adventure, but she wants to warn you that this last

system is "Smurfity smurf smurf!". She has a wire that is 100 inches long and cut into two pieces.
She wants you to find out if it's possible to bend one piece of wire into the shape of a square and the
other into the shape of a circle, so that the total area enclosed by the two pieces is 650 inches
squared. If this is possible, find the length of the side of the square, x, and the radius of the circle,
y. (Smurfette's Hint: Just smurf the smurf and the smurf...then smurf smurf the
smurf...and...smurf!!)

Answer 1

take x=2.515834 and r=14.31386

Explanation:

Let us call the the lenght of the side of the square as x. The total lenght of the wire is 100. Note that if we have a square of side x, it has a perimeter of 4x. That means, that we need a wire of length 4x to build a square of side x. Note that if we take a wire of length 4x, we have that the remainder is 100-4x. We will use this to form a circle. As for the square, since we are using the wire of length 100-4x to build a circle, it must happen that the perimeter of the circle is 100-4x.

Recall that the perimeter of a circle of radius r is
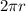`2\pi r`, so in this case , we have that
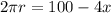`2\pi r = 100-4x` which implies that
`r =(100-4x)/(2\pi)`.

Now, recall that the area of a square of side x is
`x^2`. Also, recall that the area of a circle of radius r is
`\pi r^2`. In our case, the area of the circle is given by

`\pi r^2 = \pi ((100-4x)/(2\pi))^2`

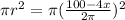
Also, we are given that the sum of the areas of both figures is 650. That is

`x^2 + \pi ((100-4x)/(2\pi))^2 = x^2+((100-4x)^2)/(4\pi)=650`

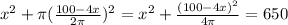
By substracting 650 on both sides and multiplying by
`4\pi` this equation is equivalent to

`4\pi x^2 + (100-4x)^2-650\cdot 4\pi =0`

if we expand
`(100-4x)^2` and then group each term of x, x^2 we get :

`(4\pi+16)x^2-800x+100^2-650\cdot 4\pi =0`

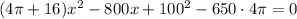
Recall that given a cuadractic equation of the form
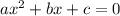`ax^2+bx+c=0` the solution is given by

`x = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a}`

In this case, the existence of a real solution is given by the expression
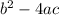`b^2-4ac`. For it to have a real solution, it must happen that
`b^2-4ac\geq 0`

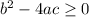
In this case, b=-800, c = 100^2-650\cdot 4\pi, a = 4\pi+16[/tex]

For this values, we get that
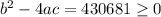`b^2-4ac = 430681\geq 0`, so the is a solution for our problem.

In this case,

`x = \frac{-b - \sqrt[]{b^2-4ac}}{2a}= 2.515834`

and
`x = \frac{-b + \sqrt[]{b^2-4ac}}{2a}= 25.4891` are the two possible solutions for this problem. We can check that this values of x fulfill our restrictions. Note that if x=25.4891, by replacing in the value of r, we get that r=-0.3113853. Since r is the radius of the circle, it must be positive. Hence, x=25.4891 is discarted.For x=2.515834 we get a value of r=14.31386, so this is the answer