Answer:
h=14.9966
Explanation:
1. The formula of the volume is:
V=
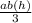
2. So you have to substitute the the data that you have:
3533.5
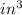 =
=
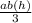
3. To have the area of the base (ab) you have to get the formula of the circle's area and solve:
A=
 (
(
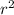 )
)
A=
 (
(
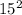 )
)
A=3.1416(225)
A=706.86in
4. Now you have the area of the base:
3533.5
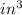 =
=
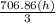
5. In this step you are going to clear the variable which is the heigh (h) and solve as an equation:
3533.5
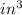 =
=
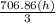
3533.5
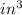 (3)=706.86(h)
(3)=706.86(h)
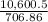 =h
=h
h=14.9966
The result may vary depending on the value of
 that you use,
that you use,