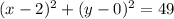Question

I need help with this please!

Answer 1

The equation of a circle using the center
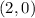`(2,0)` and the radius
`7`

`(x-2)^2+(y-0)^2= 49`

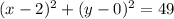
Explanation:

-Directions:

To determine the following circle on a graph, you need the to look for a point that lands exactly on the center of the circle and to find the radius, you need look for a point that lands exactly on the outline of the circle and start counting from the center, to the point. Then, use both the center and the radius for the equation of a circle. After putting the center and radius on the equation of a circle, simplify the radius by the exponent
`2`, because according to the equation of a circle, the radius is
`r^2`.

-The equation of a circle

`(x-h)^2+(y-k)^2=r^2`

-Finding the center and the radius for the equation of a circle:

Center:
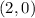`(2,0)` Radius:
`7`

`(x-2)^2+(y-0)^2= 49`