Answer:
14 inch pizza.
Explanation:
A pizza is the shape of a circle which is 360 degrees.
For the 12 in pizza, it is being divided into 60 degree slices.
360/60= 6 slices.
The area of the pizza is calculates with
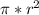 so we must find the radius of the pizza, r. 12 inch is the diameter which is 2r so half of the diameter= r.
so we must find the radius of the pizza, r. 12 inch is the diameter which is 2r so half of the diameter= r.
12/2=6=r
So the area of the 12 inch pizza is = pi*6*6= 36

36
 /6 for 6 slices means each slice is 6 pi in area.
/6 for 6 slices means each slice is 6 pi in area.
For the 14 inch pizza, it is being divided into 45 degree slices.
360/45= 8
The radius = d/2= 14/2= 7
The area =
 *7*7 = 49pi
*7*7 = 49pi
For each slice 49
 /8= 6.125
/8= 6.125

Since 6.125
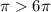 that means that the 14 inch pizza slice is a better deal because you get more food for the same amount of money.
that means that the 14 inch pizza slice is a better deal because you get more food for the same amount of money.