Question

A 10 Kg block has two forces acting on it. A rightward force of 10N and a leftward force of 7N is acting on it. What is the acceleration and which direction in m/s^2?

Answer 1

First we must write down our given portions of the problem:

Step-by-step explanation:

`m=10\text{kg}\\F_1=10\text{N}\\F_2=-7\text{N}\\`

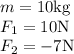
Another thing we can define is our unknowns:

`F_{\text{net}}=?\text{N}\\a_{\text{net}}=?\frac{\text{m}}{\text{s}^2}`

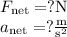
The next part of the problem would be to set up our Cartesian Coordinate System:

Positive x is positive, positive y is positive

Negative x is negative, negative y is negative

Now that we have our Cartesian Coordinate system defined one can begin to assess the problem by putting signs on the forces:

One key definition is that acceleration, and force are both vectors, therefore, we have to define their direction.

Rightward force of
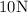`10 \text{N}\\` translates to a positive sign force because its on the positive x axis

`F_1=+10\text{N}`

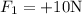
Leftward force of
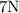`7 \text{N}` translates to a negative sign because its on the negative x axis

`F_2=-7\text{N}`

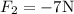
Mass is always positive.

Now we have to make use of the following law of motion the second law of motion:

`\sum F=ma_(net)`

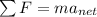
Now we will calculate the net force

:
`\sum F=(10 \text{kg})a_{\text{net}}\\F_1+F_2=(10 \text{kg})a_{\text{net}}\\\frac{(10-7)\text{N}}{10\text{kg}}=a_(net)\\a_(net)=.3\frac{\text{m}}{\text{s}^2}`

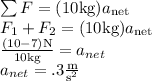
Using our Cartesian setup, and knowing since acceleration is a vector one can see that it is going in the positive x direction or to the right.

I would also like to make note of that typically people leave the units out of the problem and do the dimensional analysis to figure out the final units. Newton for force, meters per second per second is acceleration, and kilograms is for mass.