Question

The height of an object launched upward from ground level is given by the function s(t) = -4.9t2 + 78.4t, where s(t) is the height in meters and t is the time in seconds. Arrange the time intervals in ascending order of the object's magnitude of average velocity over the interval.

Answer 1

Explanation:

The height of an object launched upward from ground level is given by the function s(t) = -4.9t² +7.8t

when the object reach the ground then s(t) = 0

So; -4.9t² +7.8t = 0

-4.9t² +7.8t + 0 = 0

By using the quadratic equation

`{(-b \pm √(b^2-4ac) )/(2a)}`

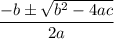
where; a = -4.9 ; b = 7.8 and c = 0

`{=(-(7.8) \pm √((7.8)^2-4(-4.9)(0)) )/(2(-4.9))}`

`{=(-(7.8) \pm √((60.84) )/(-9.8)}`

`=(-(7.8) + √((60.84) )/(-9.8) \ \ \ \ OR \ \ \ \ (-(7.8) - √((60.84) )/(-9.8)}}`

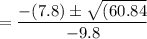
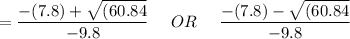
=0 OR 1.592

Hence; the distance of the object before it hits the ground after launch is t = 1.592 seconds