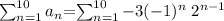Answer:
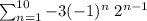
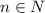
Explanation:
First, as you can see, the sequence is alternating its sign everytime, so you can deduce this term:
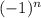
The sequence start from 3, and the following terms are the product between 3 and
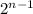 . Take a look:
. Take a look:
For n=1
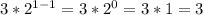
For n=2
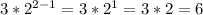
And so on...
Let's verify the formula including all terms:
Since the sequence start from 3, we must change the 3 for -3. Because
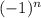 is always negative for the first term:
is always negative for the first term:
For n=1

For n=2

For n=3
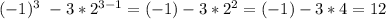
For n=4
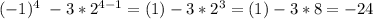
So, one possible sequence is:
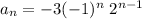
And the serie would be given by: