Answer:
5.1
Explanation:
Given that:
sample size n = 4
the mean of the original population μ is = 35
and the mean for the sample after treatment M is = 40.1
standard deviation of the sample SS = 48
The difference between the mean for the treated sample and the mean for the original population is therefore calculated as: M - μ
= 40.1 - 35
= 5.1
The standard error of M is =
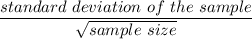
The standard error of M is =
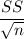
The standard error of M is =
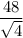
The standard error of M is =
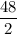
The standard error of M is = 24