Question

A manager of a grocery store wants to determine if consumers are spending

more than the national average of $150 with a standard deviation of $30. The
manager collects 10 random receipts and finds that the average customer
spends $160. He then concludes that his customers do spend more than the
national average. a) What do you see as his error in this assumption? b) How
could you redesign the study to correct it?*

Answer 1

1. The error in the assumption is taking the sample mean,
`\bar x`, as being equal to the population mean, μ

2. To correct the error, the manager will need to generate the confidence interval based on the population standard deviation on the acceptable values of the mean using the following relation;

`CI=\bar{x}\pm z(\sigma)/(√(n))`

Explanation:

We note that from the central limit theorem as the size of the sample, n, becomes more and more larger, the mean of the sample,
`\bar x`, approaches that of the population mean, μ, therefore as the grocery store manager uses the sample mean as the population mean's point estimate an error will be observed based on the size of the sample compared to the population, where the difference between the two means (the population mean and the sample mean) is
`\left | \bar{x} - \mu \right |`

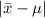
1. The error in the assumption is taking the sample mean,
`\bar x`, as being equal to the population mean, μ

2. To correct the error, the manager will need to generate the confidence interval based on the population standard deviation on the acceptable values of the mean using the following relation;

`CI=\bar{x}\pm z(\sigma)/(√(n))`

Where:

σ = Population standard deviation = $30

z = z value at 95% confidence level = 1.96

`\bar x` = Sample mean $160

n = Sample size = 10

Plugging in the values, we have;

$141.4 <
`\bar x` < $178.6

Hence the expected value of the mean should be between $141.4 and $178.6.