Question

While Mary Corens was a student at the University of Tennessee, she borrowed $9,000 in student loans at an annual interest rate of 9%. If Mary repays $1,700 per year, then how long (to the nearest year) will it take her to repay the loan? Do not round intermediate calculations. Round your answer to the nearest whole number.

Answer 1

The time required to repay the loan is 8 years.

Step-by-step explanation:

The loan amount that the student borrowed = $9000

Annual interest rate = 9%

Repayment amount per year or annuity amount = $1700 per year

Use the below formula to calculate the number of years to repay the loan amount.

A = annuity amount

r = interest rate

n = number of years

PVF = present value of annuity

`\rm PVF = (A\left [1-\left ( 1+r \right )^(-n) \right ])/(r) \\`

`9000 = (1700\left [1-\left ( 1+ 0.09 \right )^(-n) \right ])/(0.09) \\`

`9000 = 18888.9(1-1.09^(-n)) \\`

`n = 7.51 \ years \ or \ 8 \ years.`

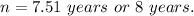
So, the time taken to repay the loan amount is 8 years.