Answer:
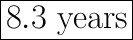
Explanation:

Applying the formula to solve for the number of years.
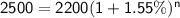
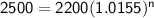
Dividing both sides by 2200.
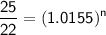
Take log of both sides and divide both sides by log(1.0155).

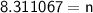
It will take 8.3 years (rounded to nearest tenth) to earn enough money to go on the trip.