Question

100 POINTS You and your best friend want to take a vacation to Australia. You have done some research and discovered that it will cost $2500 for the plane tickets, all-inclusive hotel and resort, and souvenirs. You have already saved $2200. If you invest this money in a savings account with a 1.55% interest rate compounded annually, how long will it take to earn enough money to go on the trip? Use the compound interest formula A = P (1 + i)n, where A is the accumulated amount, P is the principal, i is the interest rate per year, and n is the number of years. Round your final answer to the nearest tenth

Answer 1

`\huge \boxed{\mathrm{8.3 \ years}}`

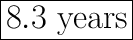
Explanation:

`\sf A=P(1+r)^n \\\\\\ A=final \ amount \\\\ P=principal \ amount \\\\ r=rate \ (\%) \\\\ n=number \ of \ years`

Applying the formula to solve for the number of years.

`\sf 2500=2200(1+1.55\%)^n`

`\sf 2500=2200(1.0155)^n`

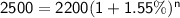
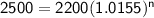
Dividing both sides by 2200.

`\sf \displaystyle (25)/(22) =(1.0155)^n`

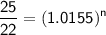
Take log of both sides and divide both sides by log(1.0155).

`\sf \displaystyle (log( (25)/(22)))/(log(1.0155)) =n`

`\sf 8.311067=n`

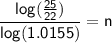
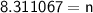
It will take 8.3 years (rounded to nearest tenth) to earn enough money to go on the trip.

Answer 2

t = 8.311 years

Explanation:

Where: t = log(A/P) / n[log(1 + r/n)]