Answer:
The missing probability is, P (X = 7) = 0.24.
Explanation:
The complete question is:
A psychology experiment on memory was conducted which required participants to recall anywhere from 1 to 10 pieces of information. Based on many results, the (partial) probability distribution below was determined for the discrete random variable (X = number of pieces of information remembered (during a fixed time period)).
What is the missing probability P(X=7)? Your answer should include the second decimal place.
X = # information | probability:
1 | 0.0
2 | 0.02
3 | 0.04
4 | 0.07
5 | 0.15
6 | 0.18
7 | ?
8 | 0.14
9 | 0.11
10 | 0.05
Solution:
The sum of the probabilities of all events of an experiment is always 1.
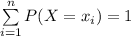
Use the above theorem to compute the missing probability.

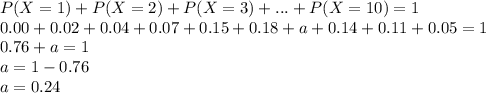
Thus, the missing probability is, P (X = 7) = 0.24.