Question

Suppose that there is a 6-sided die that is weighted in such a way that each time the die is rolled, the probabilities of rolling any number from 1 to 5 are equal, but the probability of rolling a 6 is twice the probability of rolling a 1. What are the probabilities of the 6 outcomes? What is the probability that the first roll will be an odd number and the second roll will be an even number?

Answer 1

Probabilities:

1-5:1/7

6: 2/7

Probability of even number: 4/7

Probability of odd number: 3/7

Explanation:

We are told that the probability in each throw is as follows. Probability of getting 1 to 5 is the same and the probability of 6 is twice the probability of getting 1. Let us call c the probability of having a 1. So, the probability of having 2,3,4,5 is also c. In this case, the probability of having 6 is 2*c. Since all of this outcomes are mutually exclusively, then we must have the following

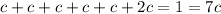`c+ c + c+ c +c + 2c = 1= 7c`(since the probabilities of mutually exclusive events that cover all outcomes of the experiment must add to 1)

This implies that
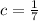`c = (1)/(7)`. Then, the probability of having a 6 is 2/7 and to have any other number is 1/7.

Each roll is independent of each other, so the probability of having an odd or even number doesn't depend of the other trials.

To calculate the probability of having an even number, we add the probabilties of getting a 2,4,6. In this case, that is 1/7+1/7+2/7 = 4/7. To calculate the probability of an odd number we add the probabilities of 1,3,5 which 1/7+1/7+1/7 = 3/7.