Question

On a coordinate plane, a line is drawn from point C to point D. Point C is at (negative 1, 4) and point D is at (2, 0). Point C has the coordinates (–1, 4) and point D has the coordinates (2, 0). What is the distance between points C and D? D = StartRoot (x 2 minus x 1) squared + (v 2 minus v 1) squared EndRoot

Answer 1

Point C has the coordinates (–1, 4) and point D has the coordinates (2, 0). What is the distance between points C and D?

d = StartRoot (x 2 minus x 1) squared + (v 2 minus v 1) squared EndRoot

5 units

Explanation:

Just did it on Edg

Answer 2

distance = 5 units

Explanation:

In order to solve this problem we can start by plotting the two points you were provided with (see attached picture). This will help us visualize the problem better.

Now, we need to find the distance between those two points, so in order to do so we can use the distance formula:

`distance = \sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

in this case the x's and y's are given by the given points, since they are written as ordere pairs. And ordered pairs are written in the form (x,y). So for Point C:

C=(-1,4)

`x_(1)=-1`

`y_(1)=4`

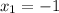
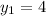
and for point D

D=(2.0)

`x_(2)=2`

`y_(2)=0`

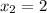
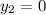
so we can now use those values in our distance formula so we get:

`d=\sqrt{(2-(-1))^(2)+(0-4)^(2)}`

`d=\sqrt{(3)^(2)+(-4)^(2)}`

`d=√(9+16)`

`d=√(25)`

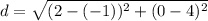
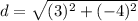
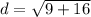
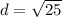
d=5 units.