Answer: 24
===========================================================
Step-by-step explanation:
We have four blank slots to fill. Call them slot A,B,C,D. There are 4 letters to pick from when filling slot A. After that selection is made, there are 3 letters left for slot B. This process keeps going til you count down to 1.
Multiplying those values out gives 4*3*2*1 = 24
-----------
Extra info:
This concept is given factorial notation of an exclamation mark, so you'd write 4! = 4*3*2*1 = 24 or simply 4! = 24.
Another example of factorial notation is 7! = 7*6*5*4*3*2*1. We start with 7 and count our way down til we get to 1, multiplying all along the way.
You could also use the nPr permutation formula
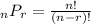 though that isn't necessary in my opinion since it involves factorials which we already used above. If you use the permutation formula, then you would have n = 4 and r = 4. The n refers to the number of items you are arranging and r = 4 is the number of slots you are filling.
though that isn't necessary in my opinion since it involves factorials which we already used above. If you use the permutation formula, then you would have n = 4 and r = 4. The n refers to the number of items you are arranging and r = 4 is the number of slots you are filling.
It turns out that
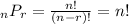 when r = n.
when r = n.
You can think of it in a smaller chunk. If we fix S to be the first letter, then we have O,N,G to rearrange. There are 6 ways to do this as shown
- ONG
- OGN
- NOG
- NGO
- GON
- GNO
Basically showing that 3! = 6. We have 4 different ways to have the first letter be selected, so we have 4*6 = 24 permutations of SONG.