Question

How many ways can you arrange SONG

Answer 1

Answer: 24

===========================================================

Step-by-step explanation:

We have four blank slots to fill. Call them slot A,B,C,D. There are 4 letters to pick from when filling slot A. After that selection is made, there are 3 letters left for slot B. This process keeps going til you count down to 1.

Multiplying those values out gives 4*3*2*1 = 24

-----------

Extra info:

This concept is given factorial notation of an exclamation mark, so you'd write 4! = 4*3*2*1 = 24 or simply 4! = 24.

Another example of factorial notation is 7! = 7*6*5*4*3*2*1. We start with 7 and count our way down til we get to 1, multiplying all along the way.

You could also use the nPr permutation formula
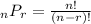`_nP_r = (n!)/((n-r)!)` though that isn't necessary in my opinion since it involves factorials which we already used above. If you use the permutation formula, then you would have n = 4 and r = 4. The n refers to the number of items you are arranging and r = 4 is the number of slots you are filling.

It turns out that
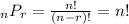`_nP_r = (n!)/((n-r)!) = n!` when r = n.

You can think of it in a smaller chunk. If we fix S to be the first letter, then we have O,N,G to rearrange. There are 6 ways to do this as shown

1. ONG
2. OGN
3. NOG
4. NGO
5. GON
6. GNO

Basically showing that 3! = 6. We have 4 different ways to have the first letter be selected, so we have 4*6 = 24 permutations of SONG.

Answer 2

Song= sngo, sogn, gnso, gosn, gnos, snog, 6 ways ?