Question

he desk has a weight of 80 lb and a centerof gravity at G. Determine the initial acceleration of a desk when the man applies enough force F to overcomethe static friction at A and B. Also, find the vertical reactions on each of the two legs at A and at B. Thecoefficients of static and kinetic friction at A andB are μs= 0.45 andμk= 0.25, respectively.

Answer 1

`N_a=(45.04)/(2)=22.52lb,N_b=(67.48)/(2) =33.74lb`

Step-by-step explanation:

Na and Nb are the vertical reactions on each of the two legs at A and at B

For the horizontal forces:

`Fcos(30)-0.5N_a-0.5N_b=0\\0.5N_a+0.5N_b= Fcos(30)\\N_a+N_b= 2Fcos(30)`

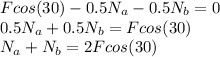
For the vertical forces:

`N_a+N_b-Fsin(30)-75=0\\N_a+N_b=Fsin(30)+80`

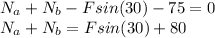
Therefore equating both equations:

`2Fcos(30)=Fsin(30)+80\\F(2cos(30)-sin(30))=80\\F=(80)/(2cos(30)-sin(30)) =64.93N`

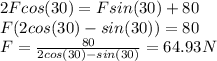
After the desk star to slide:

sum of all vertical force = ma , therefore:

`N_a+N_b-64.93sin(30)-80=0\\N_a+N_b=64.93sin(30)+80`

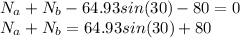
sum of all horizontal force = ma

`64.93cos(30)-0.2N_a-0.2N_b=(80lb)/(32.2ft/s^2)a\\ 0.2(N_a+N_b)=64.93cos(30)-(80lb)/(32.2ft/s^2)a\\N_a+N_b=(64.93cos(30)-(80lb)/(32.2ft/s^2)a)/(0.2)=324.65-12.42a`

equating both equations:

`324.65-12.42a=64.93sin(30)+80\\12.42a=324.65-64.93sin(30)-80\\12.42a=212.185\\a=17.08ft/s^2`

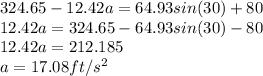
From the moment equation:

`4N_b-80(2)-64.93(3)=(-80)/(32.2) (17.08)(2)\\N_b=67.48lb`

`N_a=(64.93cos(30)-(80lb)/(32.2ft/s^2)(17.08))/(0.2)-67.48 = 45.04lb`

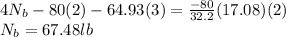
For each leg:
`N_a=(45.04)/(2)=22.52lb,N_b=(67.48)/(2) =33.74lb`