Question

Consider a Carnot heat pump cycle executed in a steady-flow system in the saturated mixture region using R-134a flowing at a rate of 0.264 kg/s. The maximum absolute temperature in the cycle is 1.15 times the minimum absolute temperature, and the net power input to the cycle is 5 kW. If the refrigerant changes from saturated vapor to saturated liquid during the heat rejection process, determine the ratio of the maximum to minimum pressures in the cycle.

Answer 1

7.15

Step-by-step explanation:

Firstly, the COP of such heat pump must be measured that is,

`COP_(HP)=(T_H)/(T_H-T_L)`

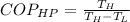
Therefore, the temperature relationship,
`T_H=1.15\;T_L`

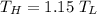
Then, we should apply the values in the COP.

`=(1.15\;T_L)/(1.15-1)`

`=7.67`

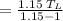
The number of heat rejected by the heat pump must then be calculated.

`Q_H=COP_(HP)* W_(nst)`

`=7.67*5=38.35`

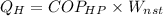
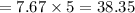
We must then calculate the refrigerant mass flow rate.

`m=0.264\;kg/s`

`q_H=(Q_H)/(m)`

`=(38.35)/(0.264)=145.27`

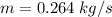
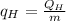
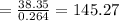
The
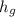`h_g` value is 145.27 and therefore the hot reservoir temperature is 64° C.

The pressure at 64 ° C is thus 1849.36 kPa by interpolation.

And, the lowest reservoir temperature must be calculated.

`T_L=(T_H)/(1.15)`

`=(64+273)/(1.15)=293.04`

`=19.89\°C`

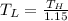
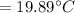
the lowest reservoir temperature = 258.703 kpa

So, the pressure ratio should be = 7.15