Find the 14th term of the geometric sequence 1 , − 5 , 25 , . . .

Question

asked Jun 24, 2021 45.1k views

2 Answers

Nekkoru · Answer 1 · 2021-06-25T20:34:46+0000

The 14th term of the geometric sequence is -1220703125.

The given sequence is geometric because each term is obtained by multiplying the previous term by a constant ratio.

In this case, the ratio between each term is -5/1 = -5.

To find the 14th term, we can use the formula for the nth term of a geometric sequence:
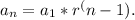
a_n = a_1 * r^(n-1).

Substituting in the values from the sequence, we have -

a_14

= 1 * (-5)^(14-1).

Simplifying, we get
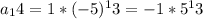
a_14 = 1 * (-5)^13 = -1 * 5^13

= -1 * 1220703125

= -1220703125.

Therefore, the 14th term of the geometric sequence is -1220703125.