Question

Use sigma notation to represent the following series for the first 10 terms.

3 + (-6) + 12 + (-24) + ⋯

Answer 1

The sum of 10 terms is S₁₀ = -1023

Explanation:

Explanation:-

Given series

3 + (-6) + 12 + (-24) + ⋯

This is geometric sequence 3 , -6 ,12 , -24 ,....

a = 3 and common ratio
`r = (-6)/(3) = -2`

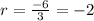
Given ratio r = -2 < 1

Sum of 'n' terms of a G.P

`S_(n) = (a(1-r^(n) ) )/(1-r) if r <1`

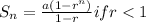
Sum of '10' terms of a G.P

`S_(10) = (3((1-(-2 )^(10) )/(1-(-2))`

`S_(10) = (3((1-(-2 )^(10) )/(3) = 1-2^(10) = 1- 1024 = - 1023`

Conclusion:-

Sum of '10' terms of a G.P = - 1023

Verification:-

The series of first 10 terms

3+(-6)+12+(-24)+48+(-96)+192+(-384)+768+(-1536) = -1023