Question

It is desired to produce and aligned carbon fiber-epoxy matrix composite having a longitudinal tensile strength of 610 MPa. Calculate (a) the critical fiber length, and (b) the volume fraction of fibers necessary if (1) the average fiber diameter is 0.029 mm, (2) the average fiber length is 2.3 mm, (3) the fiber fracture strength is 5300 MPa, (4) the fiber-matrix bond strength is 19 MPa, (5) the matrix stress at fiber failure is 17.3 MPa.

Answer 1

volume fraction of fibers is 0.4

Step-by-step explanation:

Given that for the aligned carbon fiber-epoxy matrix composite:

Diameter (D) = 0.029 mm

Length (L) = 2.3 mm

Tensile strength (
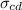`\sigma_(cd)`) = 610 MPa

fracture strength (
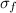`\sigma_f`) = 5300 MPa

matrix stress (
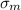`\sigma_m`) = 17.3 MPa

fiber-matrix bond strength (
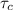`\tau_c`) = 19 MPa

The critical length is given as:

`L_C=\sigma_f((D)/(2\tau_c) )=5300*10^6((0.029*10^(-3))/(19*10^6) )=8.1*10^(-3)=8.1mm`

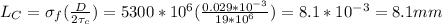
Since the critical length is greater than the length, the aligned carbon fiber-epoxy matrix composite can be produced.

The longitudinal strength is given by:

`\sigma_(cd)=(L*\tau_c)/(D) .V_f+\sigma_m(1-V_f)`

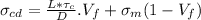
making Vf the subject of the formula:

`V_f=(\sigma_(cd)-\sigma_m)/((L*\tau_c)/(D) -\sigma_m)`

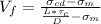
Vf is the volume fraction of fibers.

Therefore:

`V_f=(\sigma_(cd)-\sigma_m)/((L*\tau_c)/(D) -\sigma_m)=(610*10^6-17.3*10^6)/((2.3*10^(-3)*19*10^6)/(0.029*10^(-3))-17.3*10^6) } =0.4`

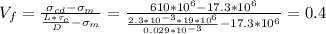
volume fraction of fibers is 0.4