Question

Manuel bought a balloon (that is a perfect sphere) with a radius of 2 \text{ cm}2 cm2, start text, space, c, m, end text. He wanted his balloon to be bigger, so he blew 222 big breaths of air into the balloon. Each big breath increased the balloon's radius by 1 \text{ cm}1 cm1, start text, space, c, m, end text.

What is the ratio of the current volume of the balloon to the original volume of the balloon?

Answer 1

The required ratio is 8

Explanation:

Volume of a sphere =
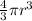`(4)/(3)\pi r^(3)` where r is the radius of the sphere.

If manuel bought a balloon (that is a perfect sphere) with a radius of 2cm, the original volume of the sphere is expressed as;

Vo =
`(4)/(3)\pi (2)^(3)`

`Vo = (4)/(3)\pi *8\\Vo = (32 \pi)/(3)`

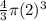
If he wanted his balloon to be bigger and he blew 2 big breaths of air into the balloon, if each big breath increased the balloon's radius by 1cm, the total radius will be the initial radius of the sphere plus the new radius after expansion.

radius of current sphere = 2cm+(1cm+1cm) = 4cm

Volume of the current sphere Vc =
`(4)/(3)\pi (4)^(3)`

`Vc = (4)/(3)\pi *64\\Vc = (256 \pi)/(3) \\`

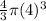
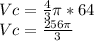
The ratio of the current volume of the balloon Vc to the original volume of the balloon Vo will be expressed as;

Vc/Vo =
`((256\pi)/(3) )/((32\pi)/(3) )`

`(Vc)/(Vo)=(256\pi)/(3)*(3)/(32\pi) \\(Vc)/(Vo)=(256)/(32)\\(Vc)/(Vo)= 8`

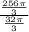
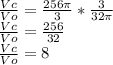
The required ratio is 8