Answer:
The amount of workdone by in emptying the tank by pumping the water over the top edge is

Step-by-step explanation:
Given that the tank is 6 feet across the top and 5 feet high.
Using the similar triangles.

5r = 3y
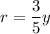
Thus; each disc is a circle with area
A =
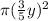
The weight of each disc is ;
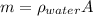
= 62.4 ×
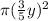
=
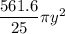
The distance pumped is 5-y
Thus; the workdone in pumping the tank by pumping the water over the top edge is :
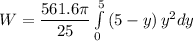
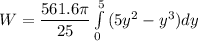
![W = (561.6 \pi)/(25)[52.083]](https://img.qammunity.org/2021/formulas/physics/high-school/sluc0gzg86kmr1qsk8mb3ihthot4nx8ck1.png)
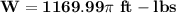
The amount of workdone by in emptying the tank by pumping the water over the top edge is
