Question

A 62.0 kg water skier at rest jumps from the dock into a 775 kg boat at rest on the east side of the dock. If the velocity of the skier is 4.50 m/s as she leaves the dock, what is the final velocity of the skier and boat?

Answer 1

v = 0.33 m/s

Step-by-step explanation:

The final velocity of the skier and boat can be calculated by conservation of the lineal momentum:

`m_(1)v_(1i) + m_(2)v_(2i) = m_(1)v_(1f) + m_(2)v_(2f)`

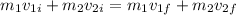
Where:

m1: is the mass of the water skier = 62.0 kg

m2: is the mass of the boat = 775 kg

v1i: is the initial velocity of the water skier = 4.50 m/s

v1f: is the final velocity of the water skier = ?

v2i: is the initial velocity of the boat = 0

v2f: is the final velocity of the boat = ?

Since the final velocity of the skier is the same that the final velocity of the boat, we have:

`m_(1)v_(1i) + m_(2)v_(2i) = m_(1)v_(f) + m_(2)v_(f)`

`m_(1)v_(1i) + 0 = v_(f)(m_(1) + m_(2))`

`v_(f) = (62.0 kg*4.50 m/s)/((62.0 kg + 775 kg))`

`v_(f) = 0.33 m/s`

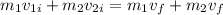
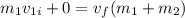
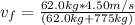
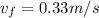
Therefore, the final velocity of the skier and boat is 0.33 m/s.

I hope it helps you!