Answer:
If we want to divide a group of N objects into K objects; we have
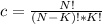
combinations
For the first group, N = 9 and K = 4
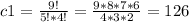
For the second group we have N = 5 (cause we already took 4 of them) and K = 3
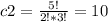
For the last group we have N =2 and K = 2, so there is only one possible combination, c3 = 1 then we have that the total number of combinations is:
C = c1*c2*c3 = 126*10*1 = 1260 possible divisions.
b)
numbers with one digit = 9, in those 9 numbers we have 9 digits.
numbers with two digits; (99 - 10 = 89) numbers, in those 89 numbers we have 2*89 = 178 digits, plus the 9 of before we have 178 + 9 = 183.
Now, for each number of 3 digits we have 3 digis obviusly, so we can write:
N*3 = 600 - 183
and N is the number of 3 digits number needed.
N = 317/3 = 139
So the 139-th number of 3 digits, this is:
100 + 139 - 1
The minus one goes because 100 is already a 3 digit number:
100 + 139 - 1 = 238
238 is the positive integer n.