Question

A dairy farmer accidentally allowed some of his cows to graze in a pasture containing weeds that would contaminate the flavor of the milk from this herd. The farmer estimates that​ there's a a 9 9​% chance of a cow grazing on some of the flavorful weeds. ​(a) Under these​ conditions, what is the probability that none of the 16 16 animals in this herd ate the tasty​ weeds? ​(b) Does the Poisson model give a good estimate of the probability that no animal ate the​ weed?

Answer 1

the required probability of is 0.1886

the approximate probability is 0.2052

Explanation:

The farmer estimates that​ there's a a 9 9​% chance of a cow grazing on some of the flavorful weeds

i.e P = 9.9% = 0.099

Let assume that X is a description of how the cows are grazing on some of the flavorful weeds.

The probability density function of the binomial distribution is :

`\mathbf{P(X=x)=(^n_x)_(p^x)(1-p)^(n-x)}`

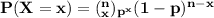
a)

To calculate that the probability that none of the 16 animals in this herd ate the tasty​ weeds.

`\mathbf{P(X=0)=(^(16) _0){(0.099)^0}(1-0.099)^(16-0)}`

=
`\mathbf{1*1*0.1886}`

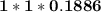
= 0.1886

Thus; the required probability of is 0.1886

b) To calculate the probability that no animal ate the weed.

By using Poisson approximation model:

`\mathbf{P(X=0) = (e^(-(np))(np)^x)/(x!) }`

`\mathbf{P(X=0) = (e^(-(16*0.099))(16*0.099)^0)/(0!) }`

`\mathbf{P(X=0) =e^(-1.584)}`

`\mathbf{P(X=0) =1.5254*10^(-7)}`

=
`\mathbf{0.2052}`

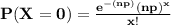
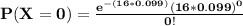
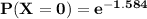
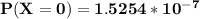
Hence; the approximate probability is 0.2052