Answer:
the required probability of is 0.1886
the approximate probability is 0.2052
Explanation:
The farmer estimates that there's a a 9 9% chance of a cow grazing on some of the flavorful weeds
i.e P = 9.9% = 0.099
Let assume that X is a description of how the cows are grazing on some of the flavorful weeds.
The probability density function of the binomial distribution is :
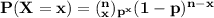
a)
To calculate that the probability that none of the 16 animals in this herd ate the tasty weeds.
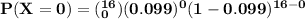
=
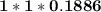
= 0.1886
Thus; the required probability of is 0.1886
b) To calculate the probability that no animal ate the weed.
By using Poisson approximation model:
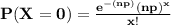
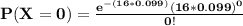
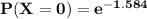
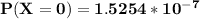
=
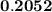
Hence; the approximate probability is 0.2052