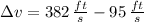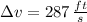Question

1. A consumer magazine tested two kinds of engines. One was a standard

engine, and it was determined that its acceleration could be modeled by

f (t) = 6 + .7t feet per square second, t seconds after starting from rest. The acceleration of the turbo-charged model could be approximated by

g(t) = 6 + 6.1 t + .05 t^2 feet per square second, t seconds after starting

from rest. How much faster is the turbo-charged model moving than the standard model at the end of a 10 second trial?

Answer 1

`\Delta v = 287\,(ft)/(s)`

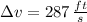
Explanation:

First, velocity function are found by means of integration, knowing that both engines start at rest and, lastly, velocities are evaluated at given time:

Standard Engine

`v_(f) = 6\cdot t +0.35\cdot t^(2)`

`v_(f) (10) = 6\cdot (10) + 0.35\cdot (10)^(2)`

`v_(f) (10) = 95\,(ft)/(s)`

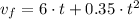
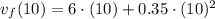
Turbocharged Engine

`v_(g) = 6\cdot t + 3.05\cdot t^(2) + 0.017\cdot t^(3)`

`v_(g) (10) = 6\cdot (10) + 3.05\cdot (10)^(2) + 0.017\cdot (10)^(3)`

`v_(g) (10) = 382\,(ft)/(s)`

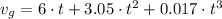
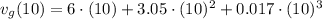
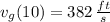
Finally, the difference of the velocity of the turbocharged model with respect to the standard one is:

`\Delta v = 382\,(ft)/(s) - 95\,(ft)/(s)`

`\Delta v = 287\,(ft)/(s)`