Question

The

equation of a circle is given by (x +3.5)2 + (y-2.82)2 = 25. What is the area of a 52° sector of this circle? Round to the nearest hundredth of square unit!

​

Answer 1

11.34 units²

Explanation:

Area of a sector is expressed as
`(\theta)/(360^(0) )*\pi r^(2)`

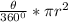
Before we can get the area of the circle, we need to find its radius. The radius of the circle can be derived from the equation of the circle given.

`(x+3.5)^(2) + (y-2.82)^(2) =25`

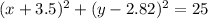
The general form of equation of a circle is given as
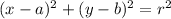`(x-a)^(2) + (y-b)^(2) =r^(2)` where r is the radius of the circle. Comparing the general equation to the given equation to get the radius r;

`r^(2) = 25\\ r = √(25)\\ r =5`

The radius of the circle is 5

Given the angle subtended by the sector of the circle to be 52°,

Area of the sector =
`(52)/(360^(0) )*\pi *5^(2)`

`= (52)/(360^(0) )*25\pi\\= 0.144 *25 \pi`

`= 0.144 * 25(3.14)\\= 0.144*78.5\\= 11.34units^(2)`

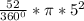
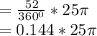
This gives the required area of the sector to nearest hundredth