Question

A data scientist tracked how many cups of coffee she drank every day at work over the course of a year. She used the data to build a probability distribution where the random variable CCC represents the number of cups of coffee she drank on a given day. Here is the distribution:

C=\# \text{ of cups}C=# of cups 000 111 222 333





P(C)P(C)P, left parenthesis, C, right parenthesis 0.050.050, point, 05 0.100.100, point, 10 0.750.750, point, 75 0.100.100, point, 10





Calculate the mean of CCC.

Answer 1

0

Explanation:

That's the answer on Khan

Answer 2

1.9

Explanation:

Given the cups of coffee drunk every day over a r]year represented by the probability distribution.

`\left|\begin{array}cC&0&1&2&3\\P(C)&0.05&0.10&0.75&0.10\end{array}\right|`

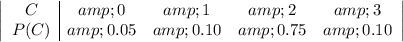
The mean number of coffee is the expected value of the probability distribution table above.

Expected Value,
`E(x)=\sum_(i=1)^(n)x_i\cdot p(x_i)`

Therefore:

E(C)=(0X0.05)+(1X0.10)+(2X0.75)+(3X0.10)

=0+0.10+1.5+0.3

Expected Value=1.9

Therefore, the mean number of coffee sold =1.9