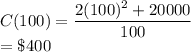Question

A fence must be built to enclose a rectangular area of 5000 ft2. Fencing material costs $1 per foot for the two sides facing north and south and $2 per foot for the other two sides. Find the cost of the least expensive fence. The cost of the least expensive fence is ___________.

Answer 1

The cost of the least expensive fence is $400

Explanation:

Let the side of the area facing north and south = x

Let the side of the area facing west and east = y.

• Area to be enclosed
  `=5000$ ft^2`
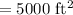
• Therefore: Area=xy=5000

Perimeter, P(x,y)=2(x+y)=2x+2y

Fencing material costs $1 per foot for the two sides facing north and south and $2 per foot for the other two sides.

Therefore, Cost of Fencing=($1 X 2x)+($2 X 2y)=

C(x,y)=2x+4y

We can write the cost function as a function of one variable by substituting for y.

Recall: xy=5000

`y=(5000)/(x)`

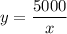
Therefore:

`C(x)=2x+4((5000)/(x) )\\C(x)=(2x^2+20000)/(x)`

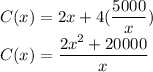
To determine the cost of the least expensive, we minimize C(x) by taking its derivative and solving for its critical points.

`C'(x)=(2x^2-20000)/(x^2)\\$When C'(x)=0\\2x^2-20000=0\\2x^2=20000\\x^2=10000\\x^2=100^2\\x=100$ ft`

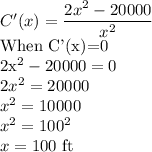
Therefore, the cost of the least expensive fence will be:

`C(100)=(2(100)^2+20000)/(100)\\=\$400`