Question

A farmer is building a fence to enclose a rectangular area against an existing wall, three of the sides will require fencing and the fourth wall area day exists. If the farmer has 100 feet of fencing, what is the largest area the farmer can enclose

Answer 1

1250 square feet

Explanation:

Let the dimensions of the wall be x and y

Since only three of the sides will require fencing

Perimeter=2x+y (where y is the side opposite the wall)

The farmer has 100 feet of fencing

Therefore: Perimeter=100 feet

2x+y=100

y=100-2x

Area of the enclosure, A(x,y)=xy

Substituting y=100-2x into A(x,y)

Area, A(x)=x(100-2x)

`A(x)=100x-2x^2`

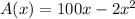
To determine the largest area the farmer can enclose, we maximize A(x) by finding its derivative and solving for its critical point.

`A'(x)=100-4x`

Set A'(x)=0

100-4x=0

4x=100

x=25 feet

Recall: y=100-2x

y=100-2(25)=50 feet

Therefore, the largest area the farmer can enclose is that of an enclosure which has dimensions 25ft X 50ft.

Maximum Area=1250 square feet