Question

A sample of 900 computer chips revealed that 58% of the chips fail in the first 1000 hours of their use. The company's promotional literature states that 54% of the chips fail in the first 1000 hours of their use. The quality control manager wants to test the claim that the actual percentage that fail is different from the stated percentage. Determine the decision rule for rejecting the null hypothesis, H0, at the 0.02 level.

Answer 1

The significance level is
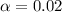`\alpha=0.02` and
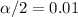`\alpha/2=0.01` we want to find the decision rule. Since is a bilateral test the critical values are:

`z_(\alpha/2)= \pm 2.326`

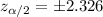
And for this case the decision rule would be reject the null hypothesis if the calculated value is:

`|t_(calculated)| >2.326`

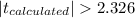
And for this case the calculated value is higher than 2.326 so then we have enough evidence to reject the null hypothesis at the significance level given.

Explanation:

Information given

n=900 represent the random sample mean

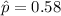`\hat p=0.58` estimated proportion of the chips fail in the first 1000 hours of their use

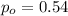`p_o=0.54` is the value to verify

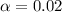`\alpha=0.02` represent the significance level

z would represent the statistic

System of hypothesis

We want to test if the actual percentage that fail is different from the stated percentage, the system of hypothesis are.:

Null hypothesis:
`p=0.54`

Alternative hypothesis:
`p \\eq 0.54`

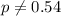
The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.58 -0.54}{\sqrt{(0.54(1-0.54))/(900)}}=2.41`

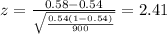
The significance level is
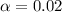`\alpha=0.02` and
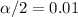`\alpha/2=0.01` we want to find the decision rule. Since is a bilateral test the critical values are:

`z_(\alpha/2)= \pm 2.326`

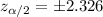
And for this case the decision rule would be reject the null hypothesis if the calculated value is:

`|t_(calculated)| >2.326`

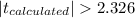
And for this case the calculated value is higher than 2.326 so then we have enough evidence to reject the null hypothesis at the significance level given.