Answer:
a) T₂ is 701.479 K
T₃ is 1226.05 K
T₄ is 2350.34 K
T₅ is 1260.56 K
b) The net work of the cycle in kJ is 2.28 kJ
c) The power developed is 114.2 kW
d) The thermal efficiency,
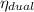 is 53.78%
is 53.78%
e) The mean effective pressure is 1038.25 kPa
Step-by-step explanation:
a) Here we have;

Where:
p₁ = Initial pressure = 95 kPa
p₂ = Final pressure =
T₁ = Initial temperature = 290 K
T₂ = Final temperature
v₁ = Initial volume
v₂ = Final volume
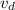 = Displacement volume =
= Displacement volume =
γ = Ratio of specific heats at constant pressure and constant volume cp/cv = 1.4 for air
r = Compression ratio = 9.1
Total heat added = 4.25 kJ
1/4 × Total heat added =
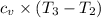
3/4 × Total heat added =
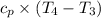
 = Specific heat at constant volume = 0.718×2.821× 10⁻³
= Specific heat at constant volume = 0.718×2.821× 10⁻³
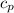 = Specific heat at constant pressure = 1.005×2.821× 10⁻³
= Specific heat at constant pressure = 1.005×2.821× 10⁻³
v₁ - v₂ = 2.2 L
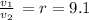
v₁ = v₂·9.1
∴ 9.1·v₂ - v₂ = 2.2 L = 2.2 × 10⁻³ m³
8.1·v₂ = 2.2 × 10⁻³ m³
v₂ = 2.2 × 10⁻³ m³ ÷ 8.1 = 2.72 × 10⁻⁴ m³
v₁ = v₂×9.1 = 2.72 × 10⁻⁴ m³ × 9.1 = 2.47 × 10⁻³ m³
Plugging in the values, we have;
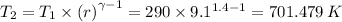
From;
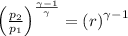 we have;
we have;
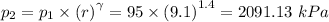
1/4×4.25 =
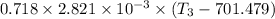
∴ T₃ = 1226.05 K
Also;
3/4 × Total heat added =
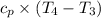 gives;
gives;
3/4 × 4.25 =
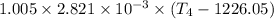 gives;
gives;
T₄ = 2350.34 K
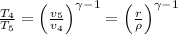
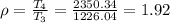
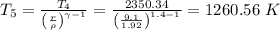
b) Heat rejected =
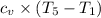
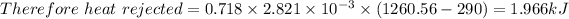
The net work done = Heat added - Heat rejected
∴ The net work done = 4.25 - 1.966 = 2.28 kJ
The net work of the cycle in kJ = 2.28 kJ
c) Power = Work done per each cycle × Number of cycles completed each second
Where we have 3000 cycles per minute, we have 3000/60 = 50 cycles per second
Hence, the power developed = 2.28 kJ/cycle × 50 cycle/second = 114.2 kW
d)
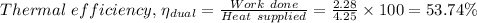
The thermal efficiency,
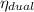 = 53.78%
= 53.78%
e) The mean effective pressure,
 , is found as follows;
, is found as follows;
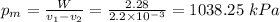
The mean effective pressure = 1038.25 kPa.