Answer:
(D)Events A and B are dependent, because P(B)≠P(B|A).
Explanation:
Definition: Two events are independent if
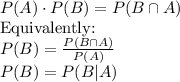
An experiment consists of rolling a standard six-sided die once.
Event A is "rolling an even number"
Even numbers are 2,4 and 6
Event B is "rolling a 2."
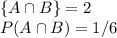
Substitution into
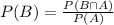
Left Hand Side =1/6
Right Hand Side =(1/6)÷(1/2)=1/3
Since
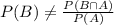 , therefore
, therefore
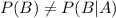 which makes the events dependent.
which makes the events dependent.