Answer:
The height of the highest point of the arch is 3 feet.
Step-by-step explanation:
The complete question is:
A dome tent’s arch is modeled by y= -0.18(x-6)(x+6) where x and y are measured in feet. To the nearest foot, what is the height of the highest point of the arch.
Solution:
The expression provided is:
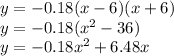
The equation is of a parabolic arch.
The general equation of a parabolic arch is:

So,
a = -0.18
b = 6.48
c = 0
Highest point of the parabolic arch is the vertex of the parabolic equation if a < 0 .
As a = -0.18 < 0, the ordinate of vertex of equation will give the height of highest point of arch.
For a parabola the abscissa of vertex is given as follows:
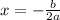
⇒
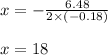
Compute the value of y as follows:
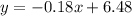
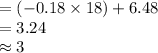
Thus, the height of the highest point of the arch is 3 feet.