Question

The height of a cone is twice the radius of its base.

What expression represents the volume of the cone, in cubic
units?
1. 2/3 pix^3
2. 4/3 pix^2
3. 2pix^3
4.4pi x^3​

Answer 1

The correct answer is option 1.
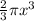`(2)/(3) \pi x^3` cubic units.

Explanation:

The formula for the volume, V of a right angled cone is given as:

`V = (1)/(3) \pi r^(2) h ...... (1)`

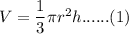
Where,
`\pi = 3.14`

`r` is the radius of the circular base of the cone.

`h` is the height of the cone.

We are given that height is twice of the radius of its base.

Let the radius of base =
`x` units

Now, As per the question statement,

The height of cone=
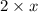`2 * x` units

Putting the values of
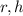`r, h` in equation (1) to find the volume:

`\Rightarrow (1)/(3) * \pi * x^(2) * 2x\\\Rightarrow (2)/(3)\pi x^(3)`

Hence, the correct answer is option 1.
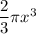`(2)/(3)\pi x^(3)` cubic units.