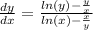Question

54. Find
`y^(\prime)` if
`x^y=y^x\text{.}`

Answer 1

Explanation:

Take the natural log of both sides:

`ln ({x}^(y) ) = ln ({y}^(x) )`

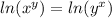
Logarithm rules allow you to bring down the exponents:

`yln(x) = xln(y)`

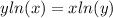
Now differentiate. We will have to implicitly differentiate 'y' since it is a function of 'x'. Both sides require the product rule:

`(dy)/(dx) ln(x) + (y)/(x) = ln(y) + (x)/(y) (dy)/(dx)`

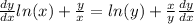
Isolate the terms that have y' since that is what we want:

`(dy)/(dx) ln(x) - (x)/(y) (dy)/(dx)= ln(y) - (y)/(x)`

Factor out y' to get:

`(dy)/(dx)( ln(x) - (x)/(y))= ln(y) - (y)/(x)`

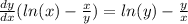
Therefore:

`(dy)/(dx) = (ln(y) - (y)/(x) )/(ln(x) - (x)/(y) )`