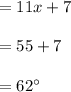Question

Given: circle k(O)

m∠R = (12x+1)
m
FP= (11x+7)
PQ= 60°
Find: measure angle FP

Answer 1

measure angle FP is 62°

Explanation:

The angle R inscribes the arc FQ, so using the property of inscribed angles in a circle, we have that:

m∠R = mFQ / 2

The arc FQ is the sum of the arcs FP and PQ, so we have:

mFQ = mFP + mPQ = 11x + 7 + 60 = 11x + 67

Now, with the first equation, we have:

`12x + 1 = (11x + 67) / 2\\\\24x + 2 = 11x + 67\\\\13x = 65\\\\x = 5^\circ`

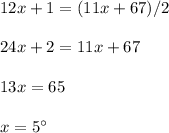
So we have that mFP

`= 11x + 7 \\\\= 55 + 7 \\\\= 62^\circ`