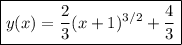Question

2y'y"=1 , y(0)=2 , y'(0)=1​

Answer 1

The left side is the derivative of
`(y')^2`:

`\left((y')^2\right)'=2y'y''`

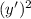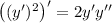
So we can integrate both sides of

`\left((y')^2\right)'=1\implies (y')^2=x+C\implies y'=\pm√(x+C)`

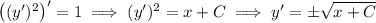
Then integrate again to solve for
`y`:

`y=\pm\frac23(x+C_1)^(3/2)+C_2`

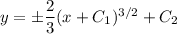
With the given initial conditions, we find

`y(0)=2\implies 2=\pm\frac23{C_1}^(3/2)+C_2`

`y'(0)=1\implies 1=\pm√(C_1)`

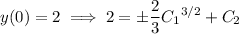
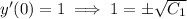
The second equation says
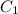`C_1` is either 1 or -1, but in the latter case, we would get
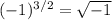`(-1)^(3/2)=√(-1)` in the first equation, which is undefined over the real numbers, so
`C_1=1`.

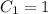So there are two candidate solutions,

`y_1=\frac23(x+1)^(3/2)+\frac43`

`y_2=-\frac23(x+1)^(3/2)+\frac83`

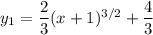
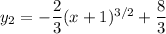
However, the second equation doesn't satisfy the initial value of the derivative, since
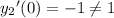`{y_2}'(0)=-1\\eq1`. So the solution is

`\boxed{y(x)=\frac23(x+1)^(3/2)+\frac43}`